MATHEMATICS S5 UNIT 10: Conditional Probability and Bayes Theorem.

Conditional probability and Bayes’ Theorem are fundamental concepts in probability theory and statistics, allowing us to update our beliefs about events based on new information.

Conditional Probability

Definition: Conditional probability is the probability of an event occurring, given that another event has already occurred. It’s about how the likelihood of one event changes when we know something new about a related event.

Notation: The conditional probability of event A given event B is denoted as $P(A|B)$, which is read as “the probability of A given B.”

Where:

• $P(A|B)$ is the probability of event A occurring given that event B has occurred.
• $P(A\cap B)$ is the joint probability of both events A and B occurring.
• $P(B)$ is the probability of event B occurring.

Conditional probability and Bayes’ Theorem are fundamental concepts in probability theory and statistics, allowing us to update our beliefs about events based on new information.

Conditional Probability

Definition: Conditional probability is the probability of an event occurring, given that another event has already occurred. It’s about how the likelihood of one event changes when we know something new about a related event.

Notation: The conditional probability of event A given event B is denoted as $P(A|B)$, which is read as “the probability of A given B.”

Formula: The formula for conditional probability is: P(A∣B)=P(B)P(A∩B)​

Where:

• $P(A|B)$ is the probability of event A occurring given that event B has occurred.
• $P(A\cap B)$ is the joint probability of both events A and B occurring.
• $P(B)$ is the probability of event B occurring.

Intuition: Think of it as narrowing down your sample space. If you know event B has happened, you only consider the outcomes where B is true. Then, among those outcomes, you find the proportion where A is also true.

Examples:

• Drawing cards: What is the probability of drawing a King given that you’ve drawn a face card? (The sample space is reduced to just face cards).
• Medical testing: What is the probability that a person has a disease given that they tested positive for it?
• Weather forecasting: What is the probability of rain tomorrow given that it’s cloudy today?

Bayes’ Theorem

Definition: Bayes’ Theorem is a mathematical rule that allows us to update the probability of a hypothesis ($A$) given new evidence ($B$). It’s essentially a way to “invert” conditional probabilities, letting us find $P(A|B)$ when we might more easily know $P(B|A)$.

Formula: Bayes’ Theorem is derived directly from the definition of conditional probability:

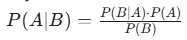
Where:

• $P(A|B)$ is the posterior probability of hypothesis A given evidence B. This is what we want to find – our updated belief.
• $P(B|A)$ is the likelihood, the probability of observing evidence B if hypothesis A is true.
• $P\left(A\right)$ is the prior probability of hypothesis A, our initial belief about A before seeing any evidence.
• $P\left(B\right)$ is the marginal probability of evidence B, the total probability of observing B (which can be calculated using the law of total probability: P(B)=P(B∣A)P(A)+P(B∣A′)P(A′) where A′ is the complement of $A$).

Intuition: Bayes’ Theorem provides a structured way to combine our prior knowledge (prior probability) with new data (likelihood) to arrive at an updated and more informed belief (posterior probability). It’s about how new evidence changes our confidence in a hypothesis.

Applications: Bayes’ Theorem has widespread applications across various fields:

• Spam filtering: Classifying emails as spam or not based on keywords.
• Medical diagnosis: Determining the probability of a disease given a positive test result, taking into account the disease’s prevalence and test accuracy.
• Financial forecasting: Assessing the risk and return of investments.
• Machine learning: Used in algorithms for classification and prediction (e.g., Naive Bayes classifier).
• Forensic science: Interpreting DNA evidence.
• Weather forecasting: Improving the accuracy of predictions by incorporating new data.