MATHEMATICS S6 UNIT 2: Logarithmic and Exponential Functions.

Exponential functions and logarithm functions are important in both theory and practice. In this unit we look at the graphs of exponential and logarithm functions, and see how they are related. In order to master the techniques explained here it is vital that you undertake plenty of practice exercises so that they become second nature. After reading this text, and/or viewing the video tutorial on this topic, you should be able to:

• specify for which values of a the exponential function f(x) = a ^x may be defined, 

• recognize the domain and range of an exponential function,

• identify a particular point which is on the graph of every exponential function,

• specify for which values of the logarithm function f(x) = log a ^x may be defined,

• recognize the domain and range of a logarithm function,

• identify a particular point which is on the graph of every logarithm function,

• understand the relationship between the exponential function f(x) = e ^x and the natural logarithm function f(x) = ln x.

What are Taylor and Maclaurin Expansions?

At their core, Taylor and Maclaurin expansions are power series representations of functions.

Taylor Series: A Taylor series for a function f(x) centered at a point a is an infinite sum of terms, where each term is derived from the function’s derivatives evaluated at that single point a. The general

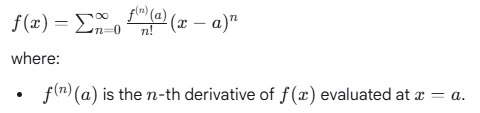
n! is the factorial of n.

(x−a)n is the n-th power of (x−a).

Maclaurin Series: A Maclaurin series is a special case of a Taylor series where the series is centered at a=0. This simplifies the formula to:

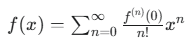
Key Concepts:

• Taylor Polynomials: The partial sum formed by the first n+1 terms of a Taylor series is called the n-th Taylor polynomial, denoted as Tn​(x). These polynomials serve as approximations of the original function. The more terms you include in the polynomial (i.e., the larger n is), the more accurate the approximation generally becomes near the center point a.
• Radius and Interval of Convergence: A Taylor series (like any power series) doesn’t necessarily converge for all values of x. It has a radius of convergence R, which defines an interval of convergence around the center a. Within this interval (a−R,a+R), the series converges to the function f(x). Outside this interval, it diverges.
• Analytic Functions: Functions that can be exactly represented by their Taylor series within their interval of convergence are called analytic functions. Most common functions (like polynomials, exponential, trigonometric, and logarithmic functions) are analytic.

Why are they important? (Applications)

Taylor and Maclaurin expansions have widespread applications across various fields of science, engineering, and mathematics:

1. Function Approximation: This is perhaps the most direct and widely used application. Complex functions can be approximated by simpler, easily computable polynomials. This is crucial for:

. Numerical Computation: Calculators and computers use Taylor polynomials to approximate values of functions like sin(x), cos(x), e^x, and ln(x).

. Physics and Engineering: Often, in physics and engineering, problems involve complex functions. Taylor series allow for simplified approximations, especially when dealing with small changes or near equilibrium points. For example, in special relativity, the Lorentz factor can be approximated using a Maclaurin series for low speeds.

. Error Estimation: Taylor’s Theorem provides a way to estimate the error (remainder) when using a finite Taylor polynomial to approximate a function.

2. Evaluating Limits: For indeterminate forms (like 0/0 or ∞/∞), Taylor series can simplify the limit calculation, often making it much easier than using L’Hopital’s Rule repeatedly.

3. Solving Differential Equations: Many differential equations cannot be solved using standard methods. Power series, including Taylor series, can be used to find series solutions to these equations.

4. Integration of Complex Functions: Some functions do not have an elementary antiderivative. By representing such functions as Taylor series, you can integrate them term by term, which often leads to a series representation of the antiderivative.

5. Understanding Function Behavior: The terms in a Taylor series provide insight into the behavior of a function near the point of expansion:

• The first term f(a) gives the value of the function.
• The second term f′(a)(x−a) relates to the linear approximation (tangent line) and the slope.

6. Complex Analysis: Taylor series are fundamental to complex analysis, where they extend the concept of function representation to complex functions.

7. Deriving Identities: Euler’s formula, e^ix =cos(x) + isin(x), is a famous example derived from the Maclaurin series of e^x, cos(x), and sin(x).