MATHEMATICS S5 UNIT 7: Matrices and Determinant of Order 3.

About Course
Matrices and determinants of order 3 are fundamental concepts in linear algebra, playing crucial roles in various mathematical and scientific applications.
I. Matrices of Order 3 (3×3 Matrices)
A matrix is a rectangular array of numbers, symbols, or expressions, arranged in rows and columns. The “order” of a matrix specifies its dimensions (number of rows number of columns).
A matrix of order 3 specifically refers to a square matrix that has 3 rows and 3 columns.
General Form: A 3×3 matrix, let’s call it , is typically represented as:

Where represents the element located in the -th row and -th column.
Key Concepts Related to 3×3 Matrices:
- Elements: The individual numbers or expressions within the matrix.
- Rows: The horizontal lines of elements.
- Columns: The vertical lines of elements.
- Main Diagonal: The elements from the top-left to the bottom-right ().
- Identity Matrix (): A special 3×3 matrix with 1s on the main diagonal and 0s elsewhere. It acts like the number ‘1’ in matrix multiplication:
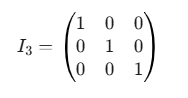
- Zero Matrix: A matrix where all elements are zero.
- Matrix Operations: You can perform operations like addition, subtraction, scalar multiplication, and matrix multiplication with 3×3 matrices, following specific rules.
Uses of 3×3 Matrices:
- Representing Systems of Linear Equations: A system of three linear equations with three variables can be compactly written as a matrix equation .
- Linear Transformations in 3D Space: Matrices can represent geometric transformations like rotations, scaling, reflections, and shears in three-dimensional space.
- Data Organization: Used in various fields (e.g., computer graphics, physics, engineering, economics) to organize and manipulate data.
II. Determinant of Order 3.
The determinant is a special scalar (a single number) value that can be computed from the elements of a square matrix. It provides crucial information about the matrix, particularly its invertibility and the geometric scaling effect of the linear transformation it represents.
The determinant of a matrix is denoted as or .
Significance of the Determinant:
- Invertibility: A square matrix is invertible (meaning its inverse A−1 exists) if and only if its determinant . If , the matrix is called singular, and it does not have an inverse.
- Systems of Linear Equations: For a system , if , there is a unique solution. If , there might be no solution or infinitely many solutions.
- Geometric Interpretation:
- In 3D space, the absolute value of the determinant of a 3×3 matrix represents the volume scaling factor of the linear transformation represented by the matrix. For example, if a transformation represented by matrix is applied to a unit cube, the volume of the transformed shape will be .
- The sign of the determinant indicates whether the transformation preserves or reverses the orientation of the space.
Methods for Calculating the Determinant of a 3×3 Matrix:
There are two primary methods for calculating the determinant of a 3×3 matrix:
-
Cofactor Expansion (Laplace Expansion): This method is generalizable to matrices of any size. To compute the determinant using cofactor expansion, you pick any row or any column. For each element in that chosen row/column, you multiply the element by its cofactor and then sum these products.
Minor (): The determinant of the submatrix formed by deleting the -th row and -th column of the original matrix. For a 3×3, minors will be determinants of 2×2 matrices.





Course Content
Square Matrices of Order 3.
-
Definitions.
12:54 -
Types of Matrices.
16:16 -
Operations on Matrices.
24:32
Matrices of Linear Transformation in 3 Dimensions.
Determinants of Order 3.
Application.
Questions and Answers.
End of Unit Assessment.
Final Unit Exam.
Student Ratings & Reviews

