MATHEMATICS S5 UNIT 1: Trigonometric Formulae, Equations and Inequalities.

Trigonometry is a branch of mathematics that studies relationships between side lengths and angles of triangles. In a broader sense, it deals with trigonometric functions and their applications. When we talk about “Trigonometric Formulae, Equations, and Inequalities,” we are diving into the core tools and problem-solving techniques within this field.

Here’s a breakdown of each component:

1. Trigonometric Formulae (Identities)

Trigonometric formulae, often called trigonometric identities, are equations that are true for all values of the variables for which the expressions are defined. They are fundamental for simplifying expressions, proving other identities, and solving trigonometric equations and inequalities.

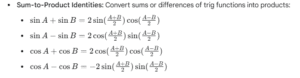
2. Trigonometric Equations

Trigonometric equations are equations that involve trigonometric functions of an unknown angle. Solving them means finding the values of the angle (or angles) that satisfy the equation. Due to the periodic nature of trigonometric functions, these equations often have infinitely many solutions.

General Steps for Solving Trigonometric Equations:

1. Simplify the Equation: Use algebraic techniques (e.g., factoring, distributing, combining like terms) and trigonometric identities to simplify the equation. The goal is often to isolate a single trigonometric function or to transform the equation into a quadratic form in terms of a trigonometric function.
2. Isolate the Trigonometric Function: Get the trigonometric function (e.g., $\sin x$, $\cos x$, $\tan x$) by itself on one side of the equation.
3. Find the Reference Angle: Determine the acute angle (often denoted as $\alpha$ or θR​) whose trigonometric value (ignoring the sign) matches the constant. This can be done using inverse trigonometric functions (e.g., $\arcsin$, $\arccos$, $\arctan$).
4. Determine Quadrants: Use the sign of the trigonometric value (positive or negative) to identify the quadrants where the solutions lie. The CAST rule or simply visualizing the unit circle is helpful here.

• Write the General Solution: Add multiples of the function’s period to each solution found in step 5 to represent all possible solutions.
  • For $\sin \theta =k$: θ=θ1​+2nπ, θ=(π−θ1​)+2nπ, where $n\in \mathbb{Z}$.
  • For $\cos \theta =k$: θ=±θ1​+2nπ, where $n\in \mathbb{Z}$.
  • For $\tan \theta =k$: θ=θ1​+nπ, where $n\in \mathbb{Z}$.
• Apply Any Domain Restrictions: If the problem specifies a particular interval for the solution, identify only the solutions that fall within that interval.

Common Solution Strategies:

• Factoring: If the equation can be factored, set each factor equal to zero.
• Using Identities: Convert expressions to a single trigonometric function or a common angle.
• Squaring Both Sides: Sometimes necessary, but beware of introducing extraneous solutions. Always check solutions in the original equation.

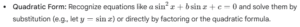
3. Trigonometric Inequalities

Trigonometric inequalities involve inequalities (like $<,>,\le ,\ge$) with trigonometric functions. Solving them means finding the range(s) of angles for which the inequality holds true.

General Approach for Solving Trigonometric Inequalities:

1. Solve the Corresponding Equation: First, treat the inequality as an equation and find all solutions within one period (e.g., $[0,2\pi )$). These solutions are critical points where the sign of the expression might change.
2. Consider the Unit Circle or Graph: This is usually the most effective method.
   • Unit Circle: Plot the critical points on the unit circle. For example, if you have $\sin x>1/2$, find the angles where $\sin x=1/2$ (which are $\pi /6$ and $5\pi /6$). Then, visualize on the unit circle where the y-coordinate (sine value) is greater than $1/2$. This will define an arc.
   • Graphing: Sketch the graph of the trigonometric function and the horizontal line representing the constant. For $\sin x>1/2$, graph $y=\sin x$ and $y=1/2$. Identify the intervals where the graph of $\sin x$ is above the line $y=1/2$.
3. Determine the Intervals: Based on the unit circle or graph, identify the intervals within one period where the inequality is satisfied. Pay close attention to whether the endpoints are included (for $\le ,\ge$) or excluded (for $<,>$). Asymptotes (for tangent, cotangent, secant, cosecant) are always excluded.
4. Write the General Solution: Add multiples of the function’s period to the endpoints of your intervals to express all solutions.
   • For example, if you find that $\pi /6<x<5\pi /6$ is the solution in $[0,2\pi )$ for $\sin x>1/2$, the general solution would be $2n\pi +\pi /6<x<2n\pi +5\pi /6$, where $n\in \mathbb{Z}$.

Important Considerations for Inequalities:

• Periodicity: Always account for the periodic nature of trigonometric functions when writing the general solution.
• Domain Restrictions: Be mindful of where the trigonometric functions are undefined (e.g., $\tan x$ at $\pi /2+n\pi$). These points will also be boundaries for your intervals.
• Sign Changes: The sign of a trigonometric expression can change at its roots (where it equals zero) and its undefined points (asymptotes).
• Transformations: If the argument of the trigonometric function is transformed (e.g., $\sin (2x)$ or $\cos (x-\pi /4)$), you’ll need to adjust the period and phase shift accordingly when finding solutions.