PHYSICS S5 UNIT 3: Forced Oscillations and Resonance of a System.

About Course
A course named “Forced Oscillations and Resonance of a System” is a fundamental topic in physics and engineering, typically building upon an understanding of simple harmonic motion. This course delves into how systems behave when subjected to external, rhythmic forces, and the critical phenomenon of resonance.
Here’s a detailed overview of what such a course would entail:
I. Review of Basic Oscillations (Briefly)
Before diving into forced oscillations, the course would likely offer a quick review or assume prior knowledge of:
- Simple Harmonic Motion (SHM): Definition, characteristics (restoring force proportional to displacement), key parameters (amplitude, period, frequency, angular frequency), equations of motion (, , ), and energy conservation in ideal SHM (kinetic vs. potential energy).
- Damped Oscillations: How realistic systems lose energy due to resistive forces (friction, air resistance). Differentiation between underdamped, critically damped, and overdamped motion, and how damping affects the amplitude of free oscillations over time.
II. Forced Oscillations (Driven Oscillations)
This section forms the core of the course:
- Definition: Introducing the concept of an external, periodic driving force acting on an oscillating system.
- Equation of Motion: Setting up the differential equation that describes a damped, driven oscillator. This is typically a second-order linear ordinary differential equation with constant coefficients.
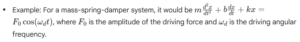
- Transient vs. Steady-State Response: Understanding that initially, the system’s response is a combination of its natural (damped) oscillation and the forced oscillation (transient part), but eventually, the system settles into oscillating at the driving frequency (steady-state part).
- Amplitude and Phase of Forced Oscillations: Deriving or analyzing the expressions for the amplitude of the steady-state oscillation and its phase relationship relative to the driving force. Students will see how these depend on the driving frequency, natural frequency, damping coefficient, and driving force amplitude.
III. Resonance
This is the central and most significant phenomenon studied in the course:
- Definition: Understanding that resonance occurs when the driving frequency matches (or is very close to) the natural frequency of the system.
- Resonance Curve (Amplitude vs. Driving Frequency): Graphically representing how the amplitude of the forced oscillation changes as the driving frequency varies.
- Effect of Damping on Resonance:
- Sharpness (Q-factor): How low damping leads to a very sharp and high resonance peak, while high damping leads to a broader and lower peak.
- Phase Shift at Resonance: Analyzing how the phase difference between the driving force and the system’s displacement changes around resonance.
- Energy Transfer at Resonance: Understanding that at resonance, energy is transferred most efficiently from the driving force to the oscillating system, leading to maximum energy absorption and maximum amplitude.
-
IV. Applications and Consequences of Resonance
This practical section emphasizes the real-world importance of these concepts:
- Beneficial Applications:
- Musical Instruments: How resonance amplifies sound in string, wind, and percussion instruments.
- Radio and TV Tuning: How resonant circuits select specific frequencies.
- Microwave Ovens: Resonant heating of water molecules.
- MRI (Magnetic Resonance Imaging): A medical diagnostic tool utilizing nuclear magnetic resonance.
- Clocks: Using precise resonance of pendulums or quartz crystals.
- Seismographs: Designed to resonate with specific earthquake frequencies.
- Destructive Consequences (Resonance Disasters):
- Structural Collapse: Famous examples like the Tacoma Narrows Bridge (though involving complex aeroelastic flutter, the principle of resonance is often illustrated).
- Earthquake Damage: How buildings can resonate with seismic waves.
- Machinery Failure: Unwanted vibrations and fatigue in engines, turbines, and other rotating machinery.
- Acoustic Resonance: Breaking glass with sound.
- Human Body: Resonant frequencies of organs or the whole body to vibrations.
- Vibration Control and Isolation: Principles used to design systems that either avoid resonance or effectively damp unwanted oscillations.
- Beneficial Applications:
Course Content
Introduction.
-
Introduction
07:19
Damped Oscillations.
Equation of Damped Oscillations.
The Solution of Equation of Damping.
Type of Damped Oscillation.
Natural Frequency of a Vibration and Forced Oscillation.
Equation of Forced Oscillation and its Solution.
Variation of Forced Frequency on Graph at Amplitude Close to Natural Frequency of Vibration.
Resonance.
Applications and Examples of Resonance in Everyday Life.
Effect of Resonance on a System
Check my Progress
END OF UNIT QUESTIONS
Final Unit Exam
Student Ratings & Reviews

