MATHEMATICS S4 UNIT 8: Limits of polynomial, rational and irrational functions.

What Will You Learn?

• • Define a Limit Informally: Explain what it means for a function's output (y-value) to approach a specific value (L) as its input (x-value) approaches a certain number (a), without necessarily reaching it.
• • Differentiate between Limit Value and Function Value: Understand that limx→af(x) is about the behavior of the function near x=a, which may or may not be the same as f(a) (the actual value of the function at x=a).
• • Interpret Limits Graphically: Estimate the limit of a function by examining its graph, including identifying cases where limits exist, do not exist, or are infinite.
• • Interpret Limits Numerically: Estimate limits by constructing and analyzing tables of function values as the input approaches a specific number from both the left and right sides.
• • Understand One-Sided Limits: Define and evaluate left-hand limits (limx→a−f(x)) and right-hand limits (limx→a+f(x)), and recognize that a two-sided limit exists if and only if both one-sided limits exist and are equal.
• • Apply Limit Laws (Properties of Limits): Use the algebraic properties of limits to evaluate limits of sums, differences, products, quotients, and powers of functions (e.g., lim(f±g), lim(c⋅f), lim(f⋅g), lim(f/g), lim(fn)).
• • Evaluate Limits of Polynomial Functions: Understand that for polynomial functions, the limit as x approaches a can usually be found by direct substitution (i.e., limx→aP(x)=P(a)).
• • Evaluate Limits of Rational Functions ( Find limits by direct substitution if the denominator is non-zero, Handle indeterminate forms, Determine limits that result in a number over zero where a number is different to zero, leading to infinite limits (±∞), and relate these to vertical asymptotes.)
• • Evaluate Limits of Irrational (Radical) Functions: Apply direct substitution and, when necessary, use rationalization techniques to evaluate limits involving square roots or other radicals.
• • Evaluate Limits at Infinity:
• Determine the behavior of polynomial, rational, and irrational functions as x approaches positive or negative infinity (limx→±∞f(x)).
• Relate limits at infinity to horizontal asymptotes of rational functions (comparing degrees of numerator and denominator).
• Identify cases where limits at infinity result in ±∞.
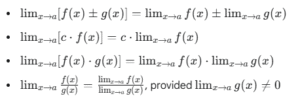
• • Apply the Squeeze Theorem (Sandwich Theorem): Use this theorem to evaluate limits of functions that are "squeezed" between two other functions with the same limit.
• Connect Limits to Continuity:
• • Define Continuity: Understand the formal definition of continuity at a point in terms of limits (i.e., f(c) is defined, limx→cf(x) exists, and limx→cf(x)=f(c)).
• • Identify Discontinuities: Classify different types of discontinuities (removable, jump, infinite) based on limit behavior.
• • Determine Continuity of Functions: Assess whether polynomial, rational, and irrational functions are continuous over their domains or at specific points.
• Develop Calculus Reasoning:
• • Lay the Foundation for Calculus: Recognize that the concept of a limit is essential for understanding the formal definitions of derivatives and integrals, which are the core topics of calculus.
• • Solve Problems: Apply their understanding of limits to solve a variety of mathematical problems and understand the basic applications of limits in describing function behavior.